ImperialViolet

Adam Langley's Weblog

Let's Kerberos (07 Apr 2024)

(I think this is worth pondering, but I don’t mean it too seriously—don’t panic.)

Are the sizes of post-quantum signatures getting you down? Are you despairing of deploying a post-quantum Web PKI? Don’t fret! Symmetric cryptography is post-quantum too!

When you connect to a site, also fetch a record from DNS that contains a handful of “CA” records. Each contains:

“CA-key” is a symmetric key known only to the CA, and “server-CA-key” is a symmetric key known to the server and the CA.

The client finds three of these CA records where the UUID matches a CA that the client trusts. It then sends a message to each CA containing:

The CA can decrypt “client-CA-key” and then it can decrypt “server-CA-key” (from the DNS information that the client sent) using an AAD that’s either the client’s specified hostname, or else that hostname with the first label replaced with *, for wildcard records.

The CA replies with Eserver-CA-key(client-server-key), i.e. the client’s chosen key, encrypted to the server. The client can then start a TLS connection with the server, send it the three encrypted client–server keys, and the client and server can authenticate a Kyber key-agreement using the three shared keys concatenated.

Both the client and server need symmetric keys established with each CA for this to work. To do this, they’ll need to establish a public-key authenticated connection to the CA. So these connections will need large post-quantum signatures, but that cost can be amortised over many connections between clients and servers. (And the servers will have to pass standard challenges in order to prove that they can legitimately speak for a given hostname.)

Some points:

Chrome support for passkeys in iCloud Keychain (18 Oct 2023)

Chrome 118 (which is rolling out to the Stable channel now) contains support for creating and accessing passkeys in iCloud Keychain.

Firstly, I’d like to thank Apple for creating an API for this that browsers can use: it’s a bunch of work, and they didn’t have to. Chrome has long had support for creating WebAuthn credentials on macOS that were protected by the macOS Keychain and stored in the local Chrome profile. If you’ve used WebAuthn in Chrome and it asked you for Touch ID (or your unlock password) then it was this. It has worked great for a long time.

But passkeys are supposed to be durable, and something that’s forever trapped in a local profile on disk is not durable. Also, if you’re a macOS + iOS user then it’s very convenient to have passkeys sync between your different devices, but Google Password Manager doesn’t cover passkeys on those platforms yet. (We’re working on it.)

So having iCloud Keychain support is hopefully useful for a number of people. With Chrome 118 you’ll see an “iCloud Keychain” option appear in Chrome’s WebAuthn UI if you’re running macOS 13.5 or later:

An image of the iCloud Keychain option in Chrome's WebAuthn UI

You won’t, at first, see iCloud Keychain credentials appear in autofill. That’s because you need to grant Chrome permission to access the metadata of iCloud Keychain passkeys before it can display them. So the first time you select iCloud Keychain as an option, you’ll see this:

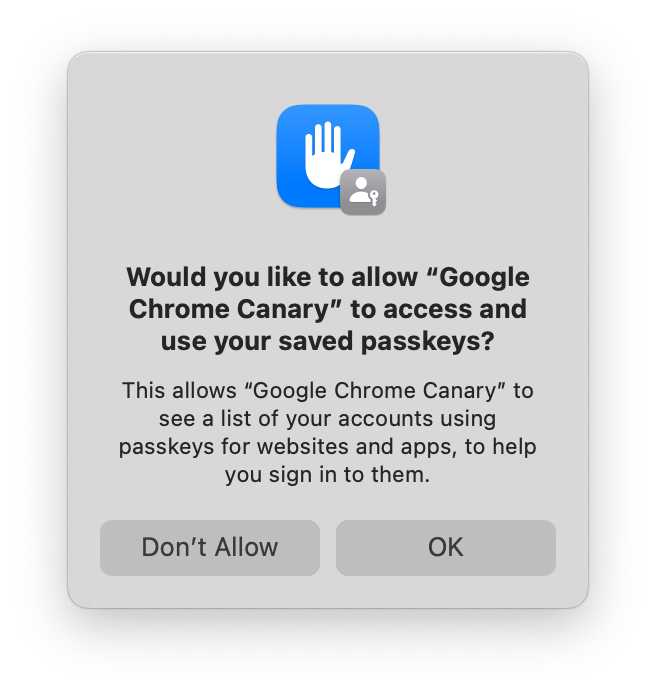
An image of the macOS passkeys permission dialog

If you accept, then iCloud Keychain credentials will appear in autofill, and in Chrome’s account picker when you click a button to use passkeys. If you decline, then you won’t be asked again. You can still use iCloud Keychain, but you’ll have to go though some extra clicks every time.

You can change your mind in System Settings → Passkeys Access for Web Browsers, or you can run tccutil reset WebBrowserPublicKeyCredential from a terminal to reset that permission system wide. (Restart Chrome after doing either of those things.)

Saving a passkey in iCloud Keychain requires having an iCloud account and having iCloud Keychain sync enabled. If you’re missing either of those, the iCloud Keychain passkey UI will prompt you to enable them to continue. It’s not possible for a regular process on macOS to tell whether iCloud Keychain syncing is enabled, at least not without gross tricks that we’re not going to try. The closest that we can cleanly detect is whether iCloud Drive is enabled. If it is, Chrome will trigger iCloud Keychain for passkey creation by default when a site requests a “platform” credential in the hope that iCloud Keychain sync is also enabled. (Chrome will default to iCloud Keychain for passkey creations on accounts.google.com whatever the status of iCloud Drive, however—there are complexities to also being a password manager.)

If you opt into statistics collection in Chrome, thank you, and we’ll be watching those numbers to see how successful people are being in aggregate with this. If the numbers look reasonable, we may try making iCloud Keychain the default for more groups of users.

If you don’t want creation to default to iCloud Keychain, there’s a control in chrome://password-manager/settings:

An image of Chrome settings

I’ve described above how things are a little complex, but the setting is just a boolean. So, if you’ve never changed it, it reflects an approximation of what Chrome is doing. But if you set it, then every case will respect that. The enterprise policy CreatePasskeysInICloudKeychain controls the same setting if you need to control this fleet-wide.

With macOS 14, other password managers are able to provide passkeys into the system on macOS and iOS. This iCloud Keychain integration was written prior to Chromium building with the macOS 14 SDK so, if you happen to install such a password manager on macOS 14, its passkeys will be labeled as “iCloud Keychain” in Chrome until we can do another update. Sorry.

Signature counters (05 Aug 2023)

If you look at the structure of the signed messages in WebAuthn you’ll notice that one of the fields is called the “signature counter”. In the previous long post I said to ignore it, which is still correct, but here’s why.

Signature counters are optional for the authenticator to implement: it’s valid for a security key not to have a signature counter, although the vast majority of them do. In that case, the counter value is always zero. But once a website has seen a non-zero value, then the security key has to ensure that the counter, for all future assertions from a given credential, is strictly increasing.

The motivation of the signature counter is that it might allow websites to detect when a security key has been cloned. Cloning a security key is supposed to be very difficult. At the very least, you should need physical access to it, and hopefully you need to spend a substantial amount of time invasively interrogating it. But, if you assume all that happened, then one could clone a security key (probably destroying it in the process), get the private key of a credential out of it, and create a working replica which could be slipped back into the possession of the legitimate user, leaving them unaware that anything has happened. At this point, the attacker can create assertions at will because they know the credential’s private key.

If all that has happened, then the signature counter might uncover it. Unless the attacker can know exactly when the legitimate user has created an assertion, and thus incremented the counter, then eventually either they or the real user will create an assertion where the counter didn’t increase.

You might be able to tell, but I consider this a rather far-fetched scenario. Nevertheless, if a website wants to use the signature counters, then it must treat any non-incrementing counter as a signal to lock the account and trigger an investigation. At a minimum, the security key in question should be replaced. Simply rejecting the assertion is meaningless: the attacker will just increment the counter and try again, and a regular user will assume that it’s some temporary glitch and do the same.

However, where I’ve seen sites bothering to check the signature counter, they’ve always just treated it as a transient error. And I’ve never heard of a signature counter actually being used to catch an attack.

On the other hand, many security keys only have a single, global signature counter, and this allows different websites to correlate the use of the same security key between them. That is, the current counter value of your security key is somewhat identifying and can be combined with information about how often you use it. For that reason, some security keys implement more granular signature counters, and good for them, but I consider it rather a waste.

When passkeys are synced between machines, they never implement signature counters because that would require that the set of machines maintain a coherent value. So, over time, you’ll probably observe that the majority of credentials don’t have them.

Voice recognition (29 Jul 2023)

Update: Evan let me know that Whisper solved the voice recognition problem. He has a wrapper that records from a microphone and prints the transcription here. Whisper is very impressive and the only caveat is that it sometimes inserts whole fabricated sentences at the end. The words always sort of make sense in context, but there were no sounds that could possibly have caused it. It's always at the very end in my experience, and it's no problem to remove it so, with that noted, you should ignore everything below because Whisper is a better answer.

Last week’s blog post was rather long, and had a greater than normal number of typos. (Thanks to people who pointed them out. I think I’ve fixed all the ones that were reported.)

This was because I saw in reviews that iOS 17’s voice recognition was supposed to be much improved, and I figured that I’d give it a try. I’ve always found iOS’s recognition to be superior to Google Docs and I have an old iPad Pro that’s good for betas.

iOS’s performance remains good and, yes, I think it’s better than iOS 16. But it’s still hardly at the level of “magic”, especially when using technical terms. Here’s a paragraph taken directly from the raw output of last week’s post (I’ve highlighted errors with italics):

It is integrated into the W3C credential management specification and so it is called via navigator . credentials . create and navigator .credentials. get. This document is about understanding the deeper structures that underpin web orphan rather than being a guy as to its details. So we will leave a great many details to the numerous guides to Web Oran that already exist on the web and instead focus on how structures from UF were carried over into Web orphan and updated.

While it’s nice that many of the words are there, with that density of errors doing all the corrections means that it’s not clearly better than typing things out. However, the world is all aflutter about LLMs these days. Can they help?

I wrote a script to chunk paragraphs of text so that the chunks were at least 500 bytes, and then to send them to gpt-3.5-turbo with the following instructions prefixed, and a temperature of 0.6:

The following is the output of a poor speech recognition system. Please correct its errors and reply with the corrected version without any preamble. Some of the uncommon words that the system can’t recognise are U2F, CTAP, FIDO, CTAP2, JSON, FIDO2, WebAuthn, bearer token, hash, phishing, RP ID, passkey, caBLE, and password manager.

Here’s the cleaned up version of that paragraph.

It is integrated into the W3C credential management specification and so it is called via navigator.credentials.create and navigator.credentials.get. This document is about understanding the deeper structures that underpin web authentication rather than being a guide as to its details. So we will leave a great many details to the numerous guides to WebAuthn that already exist on the web and instead focus on how structures from U2F were carried over into WebAuthn and updated.

There’s one case where it wrote “web authentication” rather than “WebAuthn”, but it fixed all the other problems!

So that’s what I tried: I dictated long chunks to iOS, then ran a script to clean it up with GPT, then edited it manually in Obsidian. From Obsidian, pandoc converted to HTML and EPUB formats.

That prompt is the result of some experimentation. Initially, I asked GPT to fix “errors and grammar” but, when reading the results, some sentences were incorrect and I found that it had “fixed” them into nonsense. Therefore I dropped “and grammar”. You can ask it to output in Markdown format, and I probably should have done that, but I was too far into manual editing by the time that I thought of it.

An oddity was that I wrote the instructions with the word “recognise” (English spelling) but then thought that it might work better with the more common American spelling (“recognize”). But that seemed to make it worse!

An obvious thing to try was to use GPT 4. However, I misread the costs of OpenAI’s API and thought that their charges were per-token, not per 1000 tokens. So with estimates that were off by three orders of magnitude, GPT 4 seemed a bit too expensive for a random experiment and I used GPT 3.5 for everything.

I didn’t write this post the same way, but this experimental worked well enough that I might try it again in the future for longer public writing.

From U2F to passkeys (23 Jul 2023)

(This post is nearing 8 000 words. If you want to throw it onto an ereader there's an EPUB version too.)

Introduction

Over more than a decade, a handful of standards have developed into passkeys—a plausible replacement for passwords. They picked up a lot of complexity on the way, and this post tries to give a chronological account of the development of the core of these technologies. Nothing here is secret; it’s all described in various published standards. However, it can be challenging to read these standards and understand how it’s meant to fit together.

The beginning: U2F

U2F stands for “Universal Second Factor”. It was a pair of standards, one for computers to talk to small removable devices called security keys, and the second a JavaScript API for websites to use them. The first standard of the pair is also called the Client to Authenticator Protocol (CTAP1), and when the term “U2F” is used in isolation, it usually refers to that. The JavaScript API, now obsolete, was generally referred to as the “U2F API”.

The goal of U2F was to eliminate “bearer tokens” in user authentication. A “bearer token” is a term of art in authentication that refers to any secret that is passed around to prove identity. A password is the most common example of such a secret. It’s a bearer token because you prove who you are by disclosing it, on the assumption that nobody else knows the secret. Passwords are not the only bearer tokens involved in computer security by a long way—the infamous cookies that all web users are constantly bothered about are another example. But U2F was focused on user authentication, while cookies identify computers, so U2F was primarily trying to augment passwords.

The problem with bearer tokens is that to use them, you have to disclose them. And knowledge of the token is how you prove your identity. So every time you prove your identity, you are handing another entity the power to impersonate you. Hopefully, the other entity is the intended counterparty and so would gain nothing from impersonating you to itself. But websites are very complicated counterparties, made up of many different parts, any one of which could be compromised to leak these tokens.

Digital signatures are preferable to bearer tokens because it’s possible to prove possession of a private key, using a signature, without disclosing that private key. So U2F allowed signatures to be used for authentication on the web.

While U2F is generally obsolete these days, it defined the core concepts that shaped how everything that came after it worked. (And there remain plenty of U2F security keys in use.) It’s also the clearest demonstration of those concepts, before things got more complex, so we’ll cover it in some detail although the following sections will use modern terminology where things have been renamed, so you’ll see different names if you look at the U2F specs.

Creating a credential

CTAP1 only includes two different commands: one to create a credential and one to get a signature from a credential. Websites make requests using the U2F JavaScript API and the browser translates them into CTAP1 commands.

Here’s the structure of the CTAP1 request for creating a credential:

Offset Size Meaning
0 1 Command code, 0x01 to register
1 2 Flags, always zero
3 2 Length of following data, always 64
5 32 SHA-256 hash of client data
37 32 SHA-256 hash of AppID

There are two important inputs here: the two hashes. The first is the hash of the “client data”, a JSON structure built by the browser. The security key includes this hash in its signed output and it’s what allows the browser (or operating system) to put data into the signed message. The JSON is provided to the website by the browser and can include a variety of things, but there are two that are worth highlighting:

Firstly, the origin that made the JavaScript call. (An origin is the protocol, hostname, and port number of a URL.) This allows the website’s server to know what origin the user was interacting with when they were using their security key, and that allows it to stop phishing attacks by rejecting unknown origins. For example, if all sign-in and account actions are done on https://accounts.example.com, then the server needs to permit that as a valid origin. But, by rejecting all other origins, phishing attacks are easily defeated.

When used outside of a web context, for example by an Android app, the “origin” will be a special URL scheme that includes the hash of the public key that signed the app. If a backend server expects users to be signing in with an app, then it must recognize that app as a valid origin value too. (You might see in some documentation that there’s an iOS scheme similarly defined but, in fact, iOS incorrectly puts a web origin into the JSON string even when the request comes from an app.)

The second value from the client data worth highlighting is called the “challenge”. This value is provided by the website and it’s a large random number. Large enough that the website that created it can be sure that any value derived from it must have been created afterwards. This ensures that any reply derived from it is “fresh” and this prevents replay attacks, where an old response is repeated and presented as being new.

There are other values in the JSON string too (e.g. the type of the message, to provide domain separation), but they’re peripheral to this discussion.

Now we’ll discuss the second hash in the request: the AppID hash. The AppID is specified by the website and its hash is forever associated with the newly created credential. The same value must be presented every time the credential is used.

A privacy goal of U2F and the protocols that followed it was to prevent the creation of credentials that span websites, and thus could be a form of “super cookie”. So the AppID hash identifies the site that created a credential and, if some other site tries to use it, it prevents them from doing so. Clearly, to be effective, the browser has to limit what AppIDs a website is allowed to use—otherwise all websites could just decide to use the same AppID and share credentials!

U2F envisioned a process where browsers could fetch the AppID (which is a URL) and parse a JSON document from it that would list other sorts of entities, like apps, that would be allowed to use an AppID. But in practice, I don’t believe any of the browsers ever implemented that. Instead, a website was allowed to use an AppID if the host part of the AppID could be formed by removing labels from the website’s origin without hitting an eTLD. That was a complicated sentence, but don’t worry about it for now. AppIDs are defunct, and we will cover this logic in more detail when we discuss their replacement in a later section.

What you should take away is that credentials have access controls, so that websites can only use their own credentials. This happens to stop most phishing attacks, but that’s incidental: the hash of the JSON from the browser is what is supposed to stop phishing attacks. Rather, the AppID should be seen as a constraint on websites.

Given those inputs, the security key generates a new credential, consisting of an ID and public–private key pair.

Registration errors

Assuming that the request is well-formed, there is only one plausible error that the security key can return, but it happens a lot! The error is called “test of user presence required”. It means that a human needs to touch a sensor on the security key. U2F was designed so that security keys could be implemented in a Java-based framework that did not allow requests to block, so the computer is expected to repeatedly send requests and, if they result in this error, to wait a short amount of time and to send them again. Security keys will generally blink an LED while the stream of requests is ongoing, and that’s a signal to the user to physically touch the security key. If a touch was registered within a short time before the request was received, then the request will be processed successfully.

This shows “user presence”, i.e. that some human actually authorised the operation. Security keys don’t (generally) have a trusted display that says what operation is being performed, but this check does stop malware from getting the security key to perform operations silently.

The registration response

Here’s what comes back from a U2F security key after creating a credential:

Offset Size Meaning
0 1 Reserved, always has value 0x05
1 65 Public key (uncompressed X9.62)
66 1 Length of credential ID (“L”)
67 variable Credential ID
67 + L variable X.509 attestation certificate
variable variable ECDSA signature

The public key field is hopefully pretty obvious: it’s the public key of the newly created credential. U2F always uses ECDSA with P-256 and SHA-256, and a P-256 point in uncompressed X9.62 format is 65 bytes long.

Next, the credential ID is an opaque identifier for the credential (although we will have more to say about it later).

Then comes the attestation certificate. Every U2F security key has an X.509 certificate that (usually) identifies the make and model of the security key. The private key corresponding to the certificate is embedded within the security key and, hopefully, is hard to extract. Every new credential is signed by this attestation certificate to attest that it was created within a specific make and model of security key.

But a unique attestation certificate would obviously become a tracking vector that identifies a given security key every time it creates a credential! Since we don’t want that, the same attestation certificate is used in many security keys and manufacturers are supposed to use the same certificate for batches of at least 100,000 security keys.

Finally, the response contains the signature, from that attestation certificate, over several fields of the request and response.

Note that there’s no self-signature from the credential. That was probably a mistake in the design, but it’s a mistake that is still with us today. In fact, if you don’t check the attestation signature then nothing is signed and you needn’t have bothered with the challenge parameter at all! That’s why you might see a challenge during registration being set to a single zero byte or other such placeholder value.

Statelessness

The vast majority (probably all?) U2F security keys don’t actually store anything when they create a credential. The credential ID that they return is actually an encrypted seed that allows the security key to regenerate the private key as needed. So the security key has a single root key that it uses to encrypt generated seeds, and those encrypted seeds are the credential IDs. Since you always need to send the credential ID to a U2F security key when getting a signature from it, no per-credential storage is necessary.

The key handle won’t just be an encryption of the seed because you want the security key to be able to ignore key handles that it didn’t generate. Also, the AppID hash needs to be mixed into the ciphertext somehow so that the security key can check it. But any authenticated encryption scheme can manage these needs.

Whenever you reset a stateless security key, it just regenerates its root key, thus invalidating all previous credentials.

Getting assertions

An “assertion” is a signature from a credential. Like we did when we covered credential creation, let’s look at the structure of a CTAP1 assertion request because it still carries the core concepts that we see in passkeys today:

Offset Size Meaning
0 1 Command code, 0x02 to get an assertion
1 2 Flags: 0x0700 for “check-only”, 0x0300 otherwise
3 2 Length of following data
5 32 SHA-256 hash of Client Data
37 32 SHA-256 hash of AppID
69 1 Length of credential ID (“L”)
70 variable Credential ID

We already know what the client data and AppID hashes are. (Although this time you definitely need a random challenge in the client data!)

The security key will attempt to decrypt the credential ID and authenticate the AppID hash. If unsuccessful, perhaps because the credential ID is from a different security key, it will return an error. Otherwise, it will check to see whether its touch sensor has been touched recently and, if so, it will return the requested assertion. (If the touch sensor hasn’t been triggered then the platform does the same polling as when creating a credential, as detailed above.)

The bytes signed by an assertion look like this:

Offset Size Meaning
0 32 SHA-256 hash of the AppID
32 1 0x1 if user-presence was confirmed, zero otherwise
33 4 Signature counter
37 32 SHA-256 hash of the Client Data

The signature covers the client data hash, and thus it covers the challenge from the website. So the website can be convinced that it is a fresh signature from the security key. Since the client data also includes the origin, the website can check that the user hasn’t been phished.

There’s also a “signature counter” field. All you need to know is that you should ignore it—the field will generally be zero these days anyway.

Transports

Most security keys are USB devices. They appear on the USB bus as a Human Interface Device (HID) and they have a special usage-page number to identify themselves.

NFC capable security keys are also quite common and frequently offer a USB connection too. When using the security key via NFC, the touch sensor isn’t used. Merely having the security key in the NFC field is considered to satisfy user presence.

There are also Bluetooth security keys. They work over the GATT protocol and their major downside is that they need a battery. For a long time, Bluetooth security keys were the only way to get a security key to work with iOS, but since iOS added native support, they’ve become much less common. (And Yubico now makes a security key with a Lightning connector.)

Connecting U2F to the web

FIDO defined a web API for U2F. I’m not going to go into the details because it’s obsolete now (and Chromium never actually implemented it, instead shipping an internal extension that sites could communicate with via postMessage), but it’s important to understand how browsers translated requests from websites into U2F commands because it’s still the core of how things work now.

When registering a security key, a website could provide a list of already registered credential IDs. The idea was that the user should not mistakenly register the same security key twice, so any security key that recognised one of the already known credential IDs should not be used to complete the registration request.

Browsers implement this by sending a series of assertion requests to each security key to see whether any of the credential IDs are valid for them. That’s why there’s a “check only” mode in the assertion request: it causes the security key to report whether the credential ID was recognised without requiring a touch.

When Chrome first implemented U2F support, any security keys excluded by this check were ignored. But this meant that they never flashed and users found that confusing—they assumed that the security key was broken. So Chrome started sending dummy registration requests to those security keys, which made them flash. If the user touched them, the created credential would be discarded. (That was presumably a strong incentive for U2F security keys to be stateless!)

When signing in, a site sends a list of known credential IDs for the current user. The browser sends a series of “check only” requests to the security keys until it finds a credential recognised by each key. Then it repeatedly sends a normal request for that credential ID until the user touches a security key. The security key that the user touches first “wins” and that assertion is returned to the website.

The need for the website to send a list of credential IDs determines the standard U2F sign-in experience: the user enters their username and password and, if recognised, then the site asks them to tap their security key. A desire to move away from this model motivated the development of the next iteration of the standards.

FIDO2

The U2F ecosystem described above satisfied the needs of second-factor authentication. But that doesn’t get rid of passwords: you still have to enter your password first and then use your security key. If passwords were to be eliminated, more was needed. So an effort to develop a new security key protocol, CTAP2, was started.

Concurrent with the development of CTAP2, an updated web API was also started. That ended up moving to the W3C (the usual venue for web standards) and became the “Web Authentication” spec, or WebAuthn for short.

Together, CTAP2 and WebAuthn constituted the FIDO2 effort.

Discoverable credentials

U2F credentials are called “non-discoverable”. This means that, in order to use them, you have to know their credential ID. “Discoverable” credentials are ones that a security key can find by itself, and thus they can also replace usernames.

A security key with discoverable credentials must dedicate storage for each of them. Because of this, you sometimes see discoverable credentials called “resident credentials”, but there is a distinction between whether the security key keeps state for a credential vs whether it’s discoverable. A U2F security key doesn’t have to be stateless, it could keep state for every credential, and its credential IDs could simply be identifiers. But those credentials are still non-discoverable if they can only be used when their credential ID is presented.

With discoverable credentials comes the need for credential metadata: if the user is going to select their account entirely client-side, then the client needs to know something like a username. So in the FIDO2 model, each credential gets three new pieces of metadata: a username, a user display name, and a user ID. The username is a human-readable string that uniquely identifies an account on a website (it often has the form of an email address). The user display name can be a more friendly name and might not be unique (it often has the form of a legal name). The user ID is an opaque binary identifier for an account.

The user ID is different from the other two pieces of metadata. Firstly, it is returned to the website when signing in, while the other metadata is purely client-side once it has been set. Also, the user ID is semantically important because a given security key will only store a single discoverable credential per website for a given user ID. Attempting to create a second discoverable credential for a website with a user ID that matches an existing one will cause the existing one to be overwritten.

Storing all this takes space on the security key, of course. And, if your security key needs to be able to run within the tight power budget of an NFC device, space might be limited. Also, the interface to manage discoverable credentials didn’t make it into CTAP 2.0 and had to wait for CTAP 2.1, so some early CTAP2 security keys only let you erase discoverable credentials by resetting the whole key!

User verification

You probably don’t want somebody to be able to find your lost security key and sign in as you. So, to replace passwords, security keys are going to have to verify that the correct user is present, not just that any user is present.

So, FIDO2 has an upgraded form of user presence called “user verification”. Different security keys can verify users in different ways. The most basic method is a PIN entered on the computer and sent to the security key. The PIN doesn’t have to be numeric—it can include letters and other symbols too—one might even call it a password if the aim of FIDO wasn’t to replace passwords. But, whatever you call it, it is stronger than typical password authentication because the secret is only sent to the security key, so it can’t leak from some far away password database, and the security key can enforce a limited number of attempts to guess it.

Some security keys do user verification in other ways. They can incorporate a fingerprint reader, or they can have an integrated PIN pad for more secure PIN entry.

RP IDs

FIDO2 replaces AppIDs with “relying party IDs” (RP IDs). AppIDs were URLs, but RP IDs are bare domain names. But otherwise, RP IDs serve the same purpose as AppIDs did in CTAP1.

We only briefly covered the rules for which websites can set which AppIDs before because AppIDs are obsolete, but it’s worth covering the rules for RP IDs in detail because of how important they are in deployments.

A site may use any RP ID formed by discarding zero or more labels from the left of its domain name until it hits an eTLD. So say that you’re https://www.foo.co.uk: you can specify an RP ID of www.foo.co.uk (discarding zero labels), foo.co.uk (discarding one label), but not co.uk because that’s an eTLD. If you don’t set an RP ID in a request then the default is the site’s full domain.

Our www.foo.co.uk example might happily be creating credentials with its default RP ID but later decide that it wants to move all sign-in activity to an isolated origin, https://accounts.foo.co.uk. But none of the passkeys could be used from that origin! The site would have needed to create them with an RP ID of foo.co.uk from the beginning to allow that.

So it’s important to carefully consider your RP ID from the outset. But the rule is not to always use the most general RP ID possible. Going back to our example, if usercontent.foo.co.uk existed, then any credentials with an RP ID of foo.co.uk could be overwritten by pages on usercontent.foo.co.uk. We can assume that foo.co.uk is checking the origin of any assertions, so usercontent.foo.co.uk can’t use its ability to set an RP ID of foo.co.uk to generate valid assertions, but it can still try to get the user to create new credentials which could overwrite the legitimate ones.

CTAP protocol changes

In addition to the high-level semantic changes outlined above, the syntax of CTAP2 is thoroughly different from the U2F. Rather than being a binary protocol with fixed or ad-hoc field lengths, it uses CBOR. CBOR, when reasonably subset, is a MessagePack-like encoding that can represent the JSON data model in a compact binary format, but it also supports a bytestring type to avoid having to base64-encode binary values.

CTAP2 replaces the polling-based model of U2F with one where a security key would wait to process a request until it was able. It also tried to create a model where the entire request would be sent by the platform in a single message, rather than having the platform iterate through credential IDs to find ones that a security key recognised. However, due to limited buffer sizes of security keys, this did not work out: the messages could end up too large, especially when dealing with large lists of credential IDs, so many requests will still involve multiple round trips between the computer and the security key to process.

While I’m not going to cover CTAP2 in any detail, let’s have a look at a couple of examples. Here’s a credential creation request:

{
  # SHA-256 hash of client data
  1: h'60EACC608F20422888C8E363FE35C9544A58B8920989D060021BC30F7323A423',
  # RP ID and friendly name of website
  2: {
    "id": "webauthn.io",
    "name": "webauthn.io"
  },
  3: {
    # User ID
    "id": h'526E4A6C5A41',
    # Username
    "name": "Fred",
    # User Display Name
    "displayName": "Fred"
  },
  4: [
    # ECDSA with P-256 is acceptable to the website
    {"alg": -7, "type": "public-key"},
    # And so is RSA.
    {"alg": -257, "type": "public-key"}
  ],
  # Create a discoverable credential.
  7: {"rk": true},
  # A MAC showing that the user has entered the correct PIN and thus
  # This request has verified the user with "PIN protocol" v1.
  8: h'4153542771C1BF6586718BCD0ECA8E96', 9: 1
}

CBOR is a binary format, but it defines a diagnostic notation for debugging, and that’s how we’ll present CBOR messages here. If you scan down the fields in the message, you’ll see similarities and differences with U2F:

Likewise, here’s an assertion request:

{
  # RP ID of the requesting website.
  1: "webauthn.io",
  # Hash of the client data
  2: h'E7870DBBA212581A536D29D38831B2B8192076BAAEC76A4B34918B4222B79616',
  # List of credential IDs
  3: [
    {"id": h'D64875A5A7C642667745245E118FCD6A', "type": "public-key"}
  ],
  # A MAC showing that the user has entered the correct PIN and thus
  # This request has verified the user with "PIN protocol" one.
  6: h'6459AF24BBDA323231CF42AECABA51CF', 7: 1
}

Again, it’s structurally similar to the U2F request, except that the list of credential IDs is included in the request rather than having the computer poll for each in turn. Since the credential that we created was discoverable, critically that list could also be empty and the request would still work! That’s why discoverable credentials can be used before a username has been entered.

With management of discoverable credentials, fingerprint enrollment, enterprise attestation support, and more, CTAP2 is quite complex. But it’s a very capable authentication ecosystem for enterprises and experts.

WebAuthn

As part of the FIDO2 effort, the WebAuthn API was completely replaced. If you recall, the U2F web API was not a W3C standard, and it was only ever implemented in Chromium as a hidden extension. The replacement, called WebAuthn, is a real W3C spec and is now implemented in all browsers.

It is substantially more complicated than the old API!

WebAuthn is integrated into the W3C credential management specification and so it is invoked in JavaScript via navigator.credentials.create and navigator.credentials.get. This document is about understanding the deeper structures that underpin WebAuthn rather than being a guide to its details. So we’ll leave them to the numerous tutorials that already exist on the web and instead focus on how structures from U2F were carried over into WebAuthn and updated.

Firstly, we’ll look at the structure of a signed assertion in WebAuthn.

Offset Size Meaning
0 32 SHA-256 hash of the RP ID
32 1 Flags
33 4 Signature counter
37 varies CBOR-encoded extension outputs
37 32 SHA-256 hash of the client data

It should look familiar because it’s a superset of the CTAP signed message format. This was chosen deliberately so that U2F security keys would function with WebAuthn. This wasn’t a given—there were discussions about whether it should be a fresh start–but ultimately there were lots of perfectly functional U2F security keys out in the world, and it seemed too much of a shame to leave them behind.

But there are changes in the details. Firstly, what was the AppID hash is now the RP ID hash. We discussed RP IDs above and, importantly, the space of AppIDs and the space of RP IDs is distinct. So since U2F security keys compare the hashes of these strings, no credential registered with the old U2F API could function with WebAuthn. From the security keys’ perspective, the hash is incorrect and so the credential can’t be used. Some complicated workarounds were needed for this, which we will touch on later.

The other changes in the assertion format come from defining additional flag bits and adding an extensions block. The most important new flag bit is the one that indicates that user verification was performed in an assertion. (WebAuthn and CTAP2 were co-developed, and so the new concept of user verification from the latter was exposed in the former.)

The extensions block was added to make the assertion format more flexible. While U2F’s binary format was pleasantly simple, it was difficult to change. Since CTAP2 was embracing CBOR throughout, it made sense that security keys be able to return any future fields that needed to be added to the assertion in CBOR format.

Correspondingly, an extension block was added into the WebAuthn requests too (although those are JavaScript objects rather than CBOR). The initial intent was that browsers would transcode extensions into CBOR, send them to the authenticator, and the authenticator could return the result in its output. However, exposing arbitrary and unknown functionality from whatever USB devices were plugged into the computer to the open web was too much for browsers, and no browser ever allowed arbitrary extensions to be passed through like that. Nonetheless, several important pieces of functionality have been implemented via extensions in the subsequent years.

The first major extension was a workaround for the transition to RP IDs mentioned above. The appid extension to WebAuthn allowed a website to assert a U2F AppID when requesting an assertion, so that credentials registered with the old U2F API could still be used. Similarly, the appidExclude extension could specify an AppID in a WebAuthn registration request so that a security key registered under the old API couldn’t be accidentally registered twice.

Overall, the transition to RP IDs probably wasn’t worth it, but we’ve done it now so it’s only a question of learning for the future.

Extensions in the signed response allow the authenticator to add extra data into the response, but the last field in the signed message, the client data hash, is carried over directly from U2F and remains the way that the browser/platform adds extra data. It gained some more fields in WebAuthn:

dictionary CollectedClientData {
    required DOMString           type;
    required DOMString           challenge;
    required DOMString           origin;
    DOMString                    topOrigin;
    boolean                      crossOrigin;
};

The centrally-important origin and challenge are still there, and type for domain separation, but the modern web is complex and often involves layers of iframes and so some more fields have been added to ensure that backends have a clear and correct picture of where the purposed sign-in is happening.

Other types of authenticator

Until now, we have been dealing only with security keys as authenticators. But WebAuthn does not require that all authenticators be security keys. Although aspects of CTAP2 poke through in the WebAuthn data structures, anything that formats messages correctly can be an authenticator, and so laptops and desktops themselves can be authenticators.

These devices are known as “platform authenticators”. At this point in our evolution, they are aimed at a different use case than security keys. Security keys are called “cross-platform authenticators” because they can be moved between devices, and so they can be used to authenticate on a brand-new device. A platform authenticator is for when you need to re-authenticate a user, that is, to establish that the correct human is still behind the keyboard. Since we want to validate a specific human, platform authenticators must support user verification to be useful for this.

And so there is a specific feature detection function called isUserVerifyingPlatformAuthenticatorAvailable (usually shortened to “isUVPAA” for obvious reasons). Any website can call this and it will return true if there is a platform authenticator on the current device that can do user verification.

The majority of WebAuthn credentials are created on platform authenticators now because they’re so readily available and easy to use.

caBLE / hybrid

While platform authenticators were great for reauthenticating on the same computer, they could never work for signing in on a different computer. And the set of people who were going to go out and buy security keys was always going to be rather small. So, to broaden the reach of WebAuthn, allowing people to use their phones as authenticators was an obvious step.

CTAP over BLE was already defined, but Bluetooth pairing was an awkward and error-prone process. Could we make phones usable as authenticators without it?

The first attempt was called cloud-assisted BLE (caBLE) and it involved the website and the phone having a shared key. A WebAuthn extension allowed the website to request that a computer start broadcasting a byte string over BLE. The idea was that the phone would be listening for these BLE adverts, would trial decrypt their contents against the set of shared keys it knew about, and (if it found a match) it would start advertising in response. When the computer saw a matching reply, it would make a Generic Attribute Profile (GATT) connection to that phone, do encryption at the application level, and then CTAP could continue as normal, all without having to do Bluetooth pairing.

This was launched as a feature specific to accounts.google.com and Chrome. For several years you could enable “Phone as a Security Key” for your Google account and it did something like that. But, despite a bunch of effort, there were persistent problems:

Firstly, listening for Bluetooth adverts in the background was difficult in the Android ecosystem. To work around this, accounts.google.com would send a notification to the phone over the network to tell it when to start listening. This was fine for accounts.google.com, but most websites can’t do that.

Second, the quality of Bluetooth hardware in desktops varies considerably, and getting a desktop to send more than one BLE advert never worked well. So you could only have one phone enrolled for this service, per account.

Lastly, but most critically, BLE GATT connections were just too unreliable. Even after a considerable amount of work to try and debug issues, the most reliable combination of phone and desktop achieved only 95% connection success—and that’s after the two devices had managed to exchange BLE adverts. In common configurations, the success rate was closer to 80% and it would randomly fail even for the people developing it. So despite trying for years to make this design work, it had to be abandoned.

The next attempt was called caBLEv2. Given all the issues with BLE in the previous iteration, caBLEv2 was designed to use the least amount of Bluetooth possible: a single advert sent from the phone to the desktop. This means that the rest of the communication went over the internet, which requires that both phone and desktop have an internet connection. This is unfortunate, but there were no other viable options. Using Bluetooth Classic presents a host of problems, and BLE L2CAP does not work from user space on Windows.

Still, using Bluetooth somewhere in the protocol is critical because it proves proximity between the two devices. If all communication was done over the Internet, then the phone has no proof that the computer it is sending the assertion to is nearby. It could be an attacker’s computer on the other side of the world. But if we can send one Bluetooth message from the phone and make the computer prove that it has received it, then all other communication can be routed over the Internet. And that is what caBLEv2 does.

It also changed the relationship between the parties. While caBLEv1 required that a key be shared between the website and the phone, caBLEv2 was a relationship between a computer and a phone. This made some user flows less smooth, but it made it much easier for smaller websites to take advantage of the capability.

In practice, caBLEv2 has worked far better, although Bluetooth problems still occur. (And not every desktop has Bluetooth.)

A caBLEv2 transaction is often triggered by a browser showing a QR code. That QR code contains a public key for the browser and a shared secret. When a phone scans it, it starts sending a BLE advert that is encrypted with the shared secret and which contains a nonce and the location of an internet server that communication can be routed through. The desktop decrypts this advert, connects to that server (which forwards messages to the phone and back), and starts a cryptographic handshake to prove that it holds the keys from the QR code and that it received the BLE advert. Once that communication channel is established, CTAP2 is run over it so that the phone can be used as an authenticator.

caBLEv2 also allows the phone to send information to the desktop that allows the desktop to contact it in the future without scanning a QR code. This depends on that same internet service, which must be able to send a notification to the phone, rather than constant BLE listening. (Although a BLE advert is sent for every transaction to prove proximity.) 

But ultimately, while the name caBLE was cute, it was also confusing. And so FIDO renamed it to “hybrid” when it was included in CTAP 2.2. So you’ll now see this called “hybrid CTAP” and the transport name in WebAuthn is hybrid.

The WebAuthn-family of APIs

WebAuthn is a web API, but people also use their computers and phones outside of a web browser sometimes. So while these contexts can’t use WebAuthn itself, a number of APIs for native apps that are similar to WebAuthn have popped up. These APIs aren’t WebAuthn, but if they produce signed messages in the same format as WebAuthn, a backend server needn’t know the difference. It’s a term that I’ve made up, but I call them “WebAuthn-family” APIs.

On Windows, webauthn.dll is a system service that reproduces most of WebAuthn for apps. (Browsers on Windows use this to implement WebAuthn, so it has to be pretty complete.) On iOS and macOS, Authentication Services does much the same. On Android, Credential Manager allows apps to pass in JSON-encoded WebAuthn requests and get JSON responses back. WebAuthn Level Three also includes support for the same JSON encoding so that backends should seamlessly be able to handle sign-ins from the web and Android apps. (WebAuthn should never have used ArrayBuffers.)

Passkeys

With hybrid and platform authenticators, people had lots of access to WebAuthn authenticators. But if you reset or lost your phone/laptop you still lost all of your credentials, same as if you reset or lost a security key. In an enterprise situation, losing a security key is resolved by going to the helpdesk. In a personal context, the advice had long been to register at least two security keys and to keep one of them locked away in a safe. But it’s awfully inconvenient to register a security key everywhere when it’s locked in a safe. So while this advice worked for protecting a tiny number of high-value accounts, if WebAuthn credentials were ever going to make a serious dent in the regular authentication ecosystem, they had to do better.

“Better” has to mean “recoverable”. People do lose and reset their phones, and so a heretofore sacred property of FIDO would have to be relaxed so that it could expand its scope beyond enterprises and experts: private keys would have to be backed up.

In 2021, with iOS 15, Apple included the ability to save WebAuthn private keys into iCloud Keychain, and Android Play Services got support for hybrid. At the end of 2022, iOS 16 added support for hybrid and, on Android, Google Password Manager added support for backing up and syncing private keys.

People now had common access to authenticators, the ability to assert credentials across devices with them, and fair assurance that they could recover those credentials. To bundle that together and give it a more friendly name, Apple introduced better branding: passkeys.

With passkeys, the world now has a widely available authentication mechanism that isn’t subject to phishing, isn’t subject to password reuse nor credential stuffing, can’t be sniffed and replayed by malicious 3rd-party JavaScript on the website, and doesn’t cause a mess when the server-side password database leaks.

There is some ambiguity about the definition of passkeys. Passkeys are synced, discoverable WebAuthn credentials. But we don’t want to exclude people who really want to use a security key, so if you would like to create a credential on a security key, we assume you know what you’re doing and the UI will refer to them as passkeys even though they aren’t synced. Also, we’re still building the ecosystem of syncing, which is quite fragmented presently: Windows Hello doesn’t sync at all, Google Password Manager can only sync between Android devices, and iCloud Keychain only works on Apple devices. So there is a fair chance that if you create a credential that gets called a passkey, it might not actually be backed up anywhere. So the definition is a little bit aspirational for the moment, but we’re working on it.

Another feature that came with the introduction of passkeys was integration into browser autofill. (This is also called “conditional UI” because of the name of a value in the W3C credential management spec.) So websites can now opt to have passkeys listed in autofill, as passwords are. This is not a long-term design! It would be weird if in 20 years websites had to have a pair of text boxes on their front page for signing in, in the same way that we use an icon of a floppy disk to denote saving. But conditional UI hopefully makes it much easier for websites to adopt passkeys, given that they are starting with a user base that is 100% password users.

If you want to understand how passkey support works on a website, see here. But remember that the core concepts stretch back to U2F: passkeys are still partitioned by an RP ID, they still have credential IDs, and there’s still the client data containing a server-provided challenge.

The future

The initial launch of passkeys didn’t have any provision for third-party password managers. On iOS and macOS, you had to use iCloud Keychain, and on Android you had to use Google Password Manager. That was expedient but never the intended end state, and with iOS 17 and Android 14, third-party password managers can save and provide passkeys.

At the time of writing, in 2023, most of the work is in building out the ecosystem that we have sketched. Passkeys need to sync to more places, and third-party password manager support needs to get fleshed out.

There are a number of topics on the horizon, however. With FIDO2, CTAP, and WebAuthn, we are asking websites to trust password managers a lot more. While password managers have long existed, usage is far from universal. But with FIDO2, by design, users have to use a password manager. We are also suggesting that with passkeys, websites might not need to use a second authentication factor. Two-factor authentication has become commonplace, but that’s because the first factor (the password) was such rubbish. With passkeys, that’s no longer the case. That brings many benefits! But it means that websites are outsourcing their authentication to password managers, and some would like some attestation that they’re doing a good job.

Next, the concept of an RP ID is central to passkeys, but it’s a very web-centric concept. Some services are mobile-only and don’t have a strong brand in the form of a domain name. But passkeys are forever associated with an RP ID, which forces apps to commit to the domain name that might well appear in the UI.

The purpose of the RP ID was to stop credentials from being shared across websites and thus becoming a tracking vector. But now that we have a more elaborate UI, perhaps we could show the user the places where credentials are being used and let the RP ID be a hash of a public key, or something else not tied to DNS.

We also need to think about the problem of users transitioning between ecosystems. People switch from Android to iOS and vice versa, and they should be able to bring their passkeys along with them.

There is a big pile of corpses labeled “tried to replace passwords”. Passkeys are the best attempt so far. Here's hoping that in five years’ time, that they’re not a cautionary tale.

There's an index of all posts and one, long page with them all too. Email: agl AT imperialviolet DOT org.